I’ve been playing a lot of Boggle recently, specifically Zynga’s Boggle with Friends (formerly called Wordstreak), and I always experience a little mischevious joy every time I encounter a vulgar or adult word in the game–especially because anatomical words are so often long and high-scoring. This got me thinking “wouldn’t it be great to win a game, but with exclusively dirty words?” This led me to write my “Dirty Boggle Solver”. I implemented it in C++ as a command line utility, which you can get from my github here, and in this post I’ll explain how it works.

Rules of Boggle

First, let me give a brief explanation of Boggle for those who haven’t played before. Boggle is played on a 4×4 grid of randomly picked letters, and the goal is to find words by stringing together adjacent letters in order. Using one letter twice is not allowed.

There are a couple variations in terms of scoring. In the original game, words were score by word length: 3-4 letters worth 1 point, 5 letter words worth 2 points, 6 letter words worth 3 points, etc. In Zynga’s Boggle with Friends, they introduce more scrabble-like scoring in that each letter is wortha specific value, and there are double-letter, triple-letter, double-word, and triple-word tiles, which multiply the score for a letter or for a whole word. There are also additional points for word length.

Players must find words in the 4×4 grid in this screenshot of a Boggle with Friends game.

Human Strategy

I first got really into Boggle in the summer of 2010, where I learned a key strategy, which is to find words-inside-of-words. For example, on its own, the word “stared” is pretty good, worth 3 points by the original rules; or in Words with Friends, 7 points for the letters and 6 points for the length, for a total of 13. However, you can earn many more words by noting that “star”, “stare”, “tar”, “tare”, “tared”, and “are” are also contained within the word. It is often easy to find an additional word by tacking on an “s”, a “d”, or an “r”. And that’s not to mention reading the word backward, where you get “rat”, “rats”, and “era”. These are great because you don’t need to spend additional time searching for words (which is the time-consuming part of Boggle).

This screenshot from Boggle with Friends includes the word “stared” — worth only 13 points by itself, but worth over 60 points when you also grab all the subwords. (ignoring multiplier tiles for these calculations)

This sub-string strategy has some similarity to the strategy I used in my solver, which I will describe next.

The Solver

As noted by the answer to this quora question, there exist about 12 billion strings on a 4×4 Boggle board. So, one naive solution to make a Boggle solver would be to check every one of those strings against a list of words and return just those that are words. This is exactly how I wrote the first version of my solver, which you can see at commit 0266cfe. In this version, the program opened a list of dirty words, stored them in a hash table, and then it recursively checked every string in a 2D array representing the board.

However, this approach can be improved upon. Consider the example of this board:

This made-up boggle board contains the word “xylem” as well as lots of paths that are not valid words.

A solver as described would first start with the X tile. It would check if “X” by itself is a word (it isn’t), and then continue. Next, it would append a tile to the string, checking if each of “XP”, “XY”, and “XL” are words. And, for each of these strings, it would continue on, appending letters and checking if the letters make a word, until it has checked every possible string. This approach causes the solver to go down too many paths. “XP” is not a word, but also there are no English words that even begin with “XP”. As a result, the solver wastes a huge amount of time exploring strings that are infeasible based on what they start with.

The optimization I used was to use a prefix tree (or trie) to guide the search. A prefix tree contains strings (or arrays of anything), where words with common prefixes share a common node.

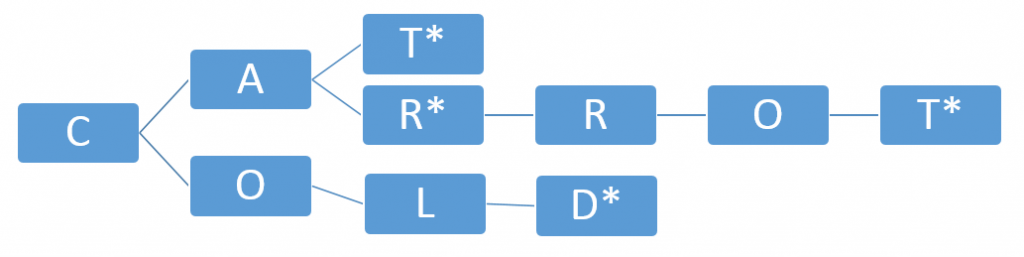
This is a prefix tree for a lexicon consisting of the words “cat”, “car”, “carrot”, and “cold”. As shown in this diagram, each letter is a node in my implementation. The star (*) indicates the end of a word; as shown by “car” and “carrot”, a node may be the end of a word while also having child nodes that lead to a longer word, also marked with a star.

First, I made the program load the list of words into a prefix tree. Then, as the program explores strings, it also checks the prefix tree to see if the current string actually has any descendents in the prefix tree of real words. If not, then the program stops exploring strings beginning with that string.

For example, in the previous example, the program would first check if “X” is a word. “X” is not a word itself; however, there are descendents in the prefix tree, implying that there are words that begin with “X” and thus that it’s worth continuing to search for strings beginning with that tile, so the program continues. However, when the program encounters “XP”, it checks the tree and finds that “P” is not a child of “X”, implying that there are no valid words that begin with “XP”. As a result, the program stops exploring paths that begin with “XP”. It then moves on to the string “XY”, exploring longer and longer strings until it finds the word “XYLEM”, but moving on quickly from paths that won’t produce words.

Result

As you can see in the repo, I made a Python script to measure the performance of the program by timing the search phase. I used the script to run 100 trials of the program at commit 0266cfe (just before adding the prefix tree) and 91b9ce9 (just after). I used the same seed both times, so even though the script generated 100 different boggle grids, the first trial used the same 100 grids as the second trial. In the commit without the prefix tree optimization, the program starts by loading the list of dirty words into a hash table, so it’s constant time to check if a string is a valid word, but the number of strings checked is much higher than with the prefix tree.

On my 2.0GHz CPU with minimal other processes running, the average solve time without the prefix tree was 8290 milliseconds; with the prefix tree, the average solve time was 8.32 milliseconds. That’s about a 1000x speedup!

Trie Implementation

As I was writing this solver, I searched for trie implementations in C++, but I didn’t find any that I liked, so I wrote my own, in trie.h. I wrote a node class, which contains information about its content (a letter), its children, and, regardless of its children, whether that node marks the end of a word. I also wrote a trie class, which contains a root node (and then the root node has child nodes, etc).

My trie class exposes methods like insert (adds a word to the trie) and searchWord (checks if a word is in the trie). However, my boggle solving program actually starts the search from each node, and only checks if there are children for that node, or if that node terminates a word, for which I expose the findChild and wordMarker methods.

I also wrote my classes to be agnostic as to the type of content actually stored — it could be a list of letters, a list of objects, whatever.

Boggle with Friends actually combines “Q” and “U” in one tile, so I made each of my nodes contain a std::string. Most nodes contain a string with only one letter, but some nodes contain the string “QU”. When loading in my list of words, my program discards any words with a single “Q”, so technically I could have just treated “Q” as an implicit “QU”; however, I felt it would be clearer if my prefix tree reflected the actual spelling of each of its word.

Usage

If you’d like to give my program a try, simply download the source from github, run make, and then run the “solver” executable in your terminal. It starts with a command-line interaction for entering the letter grid, which you can do one letter at a time.

Conclusion and Future Improvements

One thing to note about this implementation is that the program loads up a list of words when it starts. In my case, I have compiled a list of dirty, dirty words. But there is no constraint on this list; it turns out this Boggle solver is also a regular old Boggle solver if you just supply it with a full dictionary, such as /etc/whatever/words, or the official Scrabble dictionary. So go nuts!

Overall, I’m quite pleased with the result and enjoyed writing it. I also used this project as an opportunity to work on my C++ chops, so let me know if you have any style suggestions.

Here are some other ideas for future improvements:

• build the solver into an Android app to run while playing Boggle with Friends
• figure out letter probabilities in boggle or Zynga’s boggle with friends would give better statistics
• calculate scoring with the special tiles in Boggle with Friends